Encuesta :

1) Por que escogió estudiar matemáticas?


R: porque me gusto siempre la matemáticas se me hacía muy fácil incluso cuando iba en el colegio ayudaba a mis compañeros

2) Sus padres lo ayudaron a pagar sus estudios?

R: Siempre me pagaron mis estudios completos, aunque tenía becas mis padres siempre me apoyaron en todo yo solo compraba los materiales que necesitaba

3) Tuvo que esforzarse mucho para poder entrar a estudiar lo que quería?

R: obviamente estudiaba todos los días si era posible

4) Hace cuantos años que salió de la universidad?

R: hace ya 5 años

5) Le ha sido difícil encontrar trabajo?

R: no mucho

6) Cuanto tiempo lleva trabajando?

R: 5 años me puse a trabajar inmediatamente

7) Donde trabaja?

R: en concepción y el fin de semana me vengo para Santiago

8) Podría comentar si la unidad de la circunferencia es muy difícil?

R: para mí no es difícil pero solo se necesita de práctica y mucha paciencia

9) Que consejo les darías a alumnos de enseñanza media?

R: que empezaran a estudiar desde ya por si quieren un futuro estable el mundo de los “adultos” es muy distinto al que están viviendo ahora esfuércense y perseveren


encuesta realizada a: Marcos esteban fuentes martinez
edad: 28 años

Segmentos proporcionales en la circunferencia:Uno de los teoremas más importantes del trazado geométrico es el llamado Teorema de Thales, que dice lo siguiente:“Cuando dos rectas secantes son cortadas por una serie de rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes de la otra recta”.

Segmentos secante y tangentes a una circunferencia:Se denomina secante de una circunferencia a toda recta que la intersecta en dos puntos. Si una recta la intersecta en un y sólo un punto se llama tangente de la circunferencia.



Circunferencia tangentes interiores:Tienen un punto en común y los demás puntos de una de ellas están en la región interior de la otra.
Circunferencias tangentes exteriores: tienen un punto en común y los demás puntos de cada una de ellas están en la región exterior de la otra.

Semi circunferencia
es cada uno de los arcos iguales que abarca un diámetro.


ARCO
es cada una de las partes en que una cuerda divide a la circunferencia.


Diametro
es el mayor segmento inscrito; pasa por el centro y divide al círculo dos semicírculos; es la mayor de las cuerdas de la circunferencia perimetral

Cuerda
es el segmento que une los extremos de un arco.

Segmentos congruentes en una circunferencia:Dos segmentos son congruentes cuando superpuestos sus extremos coinciden, o sea son segmentos congruentes aquellos que tienen igual medida .

Si los son congruentes, entonces se escribe .

ÁNGULOS SEMI-INSCRITOS:Llamaremos ángulo semi-inscrito en una circunferencia a cualquier ángulo cuyo vértice esté en la misma circunferencia y uno de sus lados sea la tangente a la circunferencia en el vértice y otro una cuerda con origen en el vértice.

Relación con el arco que se subtiende:La medida del ángulo semi-inscrito equivale a la mitad del ángulo central que abarca del arco comprendido entre sus lados (o sea arco AB).

Ejemplo:

Dada la circunferencia de Centro O, P punto de tangencia y ángulo APT = 65º, determine Arco PQ.

A) 12,5º

B) 25º

C) 7,5º

D) 50º

E)Ninguna de las anteriores

Respuesta : alternativa D

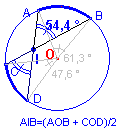
ANGULO INTERIOR en una circunferencia:Se llama Angulo interior cuando su vértice A está en un punto interior a la circunferencia (o sea en el círculo) pero no en su centro, y sus lados son dos rectas secantes.

Su medida es igual a la semisuma de los arcos que abarca BC y ED.

Ejemplo:La medida del ángulo interior es la semisuma

de los arcos que comprenden él y su opuesto

 ANGULO EXTERIOR en una circunferencia:Se llama ángulo exterior cuando su vértice A no está en la circunferencia ni en el contorno delimitado por ella, y sus lados son dos rectas secantes.

Su medida es igual a la semidiferencia de los arcos que abarca BC y ED.

Ejemplo:La medida del ángulo exterior es la semidiferencia de los arcos que abarca.